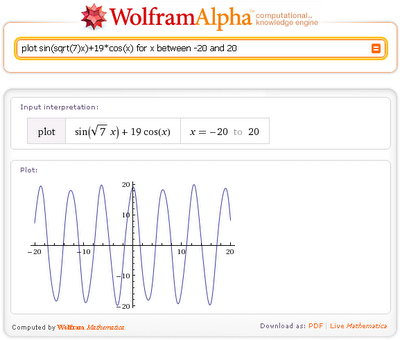
Начнем с построения простого 2-мерного графика: plot sin(sqrt(7)x)+19cos(x) для x от -20 до 20
Если заменить 7 на (-7), то получим графики действительной и мнимой частей функции: plot sin(sqrt(-7)x)+19cos(x) для x от -5 до 5

В двух предыдущих примерах мы задавали область значений аргумента х. А что будет, если мы не будем задавать область значений х?

Одной из уникальных особенностей Wolfram | Alpha является автоматический выбор подходящего диапазона х для построения графиков функций одной и двух переменных, например, как при построении графика этой функции, содержащей функции Бесселя:

Обращаясь к Wolfram | Alpha, чтобы построить график функции, мы всегда используем префикс plot. Если же мы введем какое-либо одномерное выражение без префикса plot, то получим кроме графика функции в прямоугольных декартовых координатах, еще и много других сведений об этой функции.

Сравните:

Кроме того, изображение построенного графика будет крупнее, если вы используете префикс plot.
Одновременно в Wolfram | Alpha можно строить графики нескольких функций.

Если навести мышь на левый нижний угол изображения, то становятся доступными две ссылки: Save as image и Copyable planetext. Рассмотрим такой график:

Первая ссылка Save as image, которая открывается в левом нижнем углу изображения, позволяет сохранить построенный график, как картинку на компьютере пользователя - при нажатии на Save as image автоматически начнется загрузка изображения:

Вторая ссылка Copyable planetext позволяет увидеть код, аналогичный тому, который используется системой Matematica для построения графиков:

Теперь рассмотрим, как в Wolfram | Alpha построить графики функций двух переменных. Начнем с функции y^2 cos(x) для x от -6 до 6 и y от -2 до 2

Как и в одномерном случае, Wolfram | Alpha автоматически определяет подходящий диапазон значений аргументов, где функция имеет наиболее характерный вид. В случае, если Wolfram | Alpha не может найти подходящий диапазон, то это скорее всего потому, что система не смогла определить такой диапазон, где функция имеет наиболее интересное поведение. В этом случае, мы можем задать диапазон вручную, как это было сделано выше. Посмотрите следующие примеры:
А что, если вы захотите построить одновременно несколько графиков функций двух переменных?

Wolfram | Alpha строит отдельный график для каждой функции в списке. Вот еще несколько примеров:
Во всех рассмотренных выше примерах Wolfram | Alpha строил также и контурные графики (линии уровня) в дополнение к трехмерным графикам (поверхностям). Чтобы увидеть связь между трехмерными и контурными графиками, нужно нажать кнопку “Show contour lines”. Отметим, что и трехмерные и контурные графики используют один и тот же диапазон аргументов.
Все трехмерные графики строятся с помощью функции plot3d системы Mathematica. Контурные графики были сделаны с помощью ContourPlot. В обоих случаях, чтобы увидеть код системы Mathematica для генерации изображения нужно нажать ссылку Copyable planetext в левом нижнем углу нужного изображения.
Источник by Sam Blake
Больше информации по использованию Wolfram|Alpha вы найдете в блоге

Если заменить 7 на (-7), то получим графики действительной и мнимой частей функции: plot sin(sqrt(-7)x)+19cos(x) для x от -5 до 5

В двух предыдущих примерах мы задавали область значений аргумента х. А что будет, если мы не будем задавать область значений х?

Одной из уникальных особенностей Wolfram | Alpha является автоматический выбор подходящего диапазона х для построения графиков функций одной и двух переменных, например, как при построении графика этой функции, содержащей функции Бесселя:

Обращаясь к Wolfram | Alpha, чтобы построить график функции, мы всегда используем префикс plot. Если же мы введем какое-либо одномерное выражение без префикса plot, то получим кроме графика функции в прямоугольных декартовых координатах, еще и много других сведений об этой функции.

Сравните:

Кроме того, изображение построенного графика будет крупнее, если вы используете префикс plot.
Одновременно в Wolfram | Alpha можно строить графики нескольких функций.

Если навести мышь на левый нижний угол изображения, то становятся доступными две ссылки: Save as image и Copyable planetext. Рассмотрим такой график:

Первая ссылка Save as image, которая открывается в левом нижнем углу изображения, позволяет сохранить построенный график, как картинку на компьютере пользователя - при нажатии на Save as image автоматически начнется загрузка изображения:

Вторая ссылка Copyable planetext позволяет увидеть код, аналогичный тому, который используется системой Matematica для построения графиков:

Теперь рассмотрим, как в Wolfram | Alpha построить графики функций двух переменных. Начнем с функции y^2 cos(x) для x от -6 до 6 и y от -2 до 2

Как и в одномерном случае, Wolfram | Alpha автоматически определяет подходящий диапазон значений аргументов, где функция имеет наиболее характерный вид. В случае, если Wolfram | Alpha не может найти подходящий диапазон, то это скорее всего потому, что система не смогла определить такой диапазон, где функция имеет наиболее интересное поведение. В этом случае, мы можем задать диапазон вручную, как это было сделано выше. Посмотрите следующие примеры:
А что, если вы захотите построить одновременно несколько графиков функций двух переменных?

Wolfram | Alpha строит отдельный график для каждой функции в списке. Вот еще несколько примеров:
- plot (1 - x)/(2 x + 7 y), 5 x^2 - 3y^2 + 7 x y, (x + 2 y)^4
- plot sqrt (1 + x y), sqrt (x^2 - y^2 + 2 x y)
Во всех рассмотренных выше примерах Wolfram | Alpha строил также и контурные графики (линии уровня) в дополнение к трехмерным графикам (поверхностям). Чтобы увидеть связь между трехмерными и контурными графиками, нужно нажать кнопку “Show contour lines”. Отметим, что и трехмерные и контурные графики используют один и тот же диапазон аргументов.
Все трехмерные графики строятся с помощью функции plot3d системы Mathematica. Контурные графики были сделаны с помощью ContourPlot. В обоих случаях, чтобы увидеть код системы Mathematica для генерации изображения нужно нажать ссылку Copyable planetext в левом нижнем углу нужного изображения.
Источник by Sam Blake
Больше информации по использованию Wolfram|Alpha вы найдете в блоге
Комментариев нет:
Отправить комментарий